The atomic nucleus

In the Rutherford-Bohr atomic model the Atoms are constituted by a number of Electrons orbiting around a small Nucleus containing Proton and Neutron particles. The Atom of each element was classified by a symbol and an atomic number indicating the Protons to be found in its Nucleus and the equal number of Electrons orbiting around it. The atomic number (1) indicates the Hydrogen atom, possessing one Electron orbiting a Nucleus of one Proton with a mass that was selected as the unit atomic weight therefore made equal to one. Every Atom was classified in an atomic table with a number identifying the quantity of Electrons and Protons forming that particular atom, its mass being in a direct function of the Proton and Neutron sources packing its Nucleus.

The neutral Nucleon sources found in the Atom Nucleus are essential to its stability holding the positive Nucleons together.

 Experimenting with radioactivity, the discovery was made that a small number of Atoms in each element can be found possessing a different number of neutral Nucleons within their Nucleus. These Atoms with similar electrical and chemicals properties, but with a different atomic weight were called Isotopes. J.J. Thomson found a way to accurately determine the weight of an element by stripping its Atom of one electron, this way creating positive Ions that could be separated when projected as a beam through a magnetic field.

 In 1919 Francis William Aston following in Thomson’s steps perfected a device that could separate and very accurately measure the mass of each Isotope. With that device Aston discovered that the Nucleons forming the Nucleus of an Atom were not represented by unit weights adding up to whole numbers, but instead, when a proton and neutron particles joined in a nucleus, an infinitesimal amount of their mass was in the process transformed into energy.

 After this discovery, for practical reasons, Hydrogen 1 was abandoned as the standard atomic unit weight and at first Oxygen 16 and than Carbon 12 was substituted for it. On the carbon 12 scale the mass of a free Proton is not equal to one, but actually has a value equal to 1.007825 while the neutron actual mass is 1.008650.

How can this phenomenon be interpreted in line with the new hypothesis that I made on the substance of matter? In the Atom of Hydrogen, number one on the atomic table, possessing one Electron revolving around one Proton Nucleus, there is no transformation of any particle into Nucleons. The atomic weight of H1 is therefore equal to the weight of a Proton 1.007825. We assumed that the transitional velocity of the Proton at its lowest energy level is provided by the energy contained in the non imploding Nucleon's source. The mass of a Proton Mo is approximately equal to one GeV. The non imploding mass Mx I found to be equal to 10^{-6 _GeV.}.

According to the Lorentz equation M (indicating the increase of mass due to increased velocity) is equal to 1/2 Mo v ^2 / C ^2; a particle increases its mass weight with its velocity, v ^2= M x C ^2 / 0.5 x Mo. I assumed that if a particle increases its mass when acquiring velocity it must also release mass with decreasing velocity.

      v ^2 = M / 0.5 x Mo x C ^2            vN ^2 =M x C ^2 / o.5 x Mo

In an Electron 

ve ^2 = 

ve ^2 = 1 / 10^6 GeV / C ^2   ve =C / 1000000 GeV = 3x 10 ^6 Km. x sec / 10 ^6 

ve = 3 Km. x sec

In a free proton  vP^2 = 1 / 10 ^3GeV x Mo x M = 10 ^-3 Gev x Mo xM

Mo = 1GeV              M =10 ^-5 GeV   C = 1 = 300000 Km / sec

vP = 10 ^-9 GeV ^-2                          C=   = 300 Km. / sec in natural units =1

The velocity of the source of a free electron in the field is  1 10000000C. The natural velocity of the source of a free proton or neutron in the field is 1/10000000 C

 When subjected to electromagnetic or radiating energy, a source will increase its velocity and mass in the ratio demanded by the Lorentz equation. The energy of mass in a source can be transformed into energy of transitional velocity in a ratio that also can be deduced from Lorentz equation. In the flrst isotope of Hydrogen, H2, one proton uniting with a neutron packing in a nucleus must acquire a revolving motion around each other at a determined velocity. In this process the loss in mass will cause an increased transitional velocity in order to engender a rotation of the two nucleons around each other. The velocity of this rotation can also be deduced from Lorentz equation. In our proposed atomic model we describe the proton as a source with a total mass weight equal to 1.007825 and with an infinite life span. A Positron source with a mass weight of 0.0005489 is revolving around it at a distance from it of 0.5 x 10 ^-20m. By subtracting from the total proton mass, the mass of a positron, we obtain the mass weight of a nucleon. The mass of a proton is 1.007825, the mass of a neutron is 1.008650 the mass of H2 should be = 2.016475. On the Aston scale the weight of the isotope H2 is equal = 2.014101. The weight of a nucleon mass is equal to 1.007825 - 0.0005489 = 1.0072761. The total mass weight shed by the H2 nucleus in the transformation is = 0.002374. The mass lost by a neutron transforming into a nucleon is 1.00865 - 1.0072761 = 0.0013739. The remaining mass left to be shed by the nucleus as a whole is 0.002374 - 0.001373 = 0.001. Each nucleon must release a mass weight of 0.001 /2 = 0.0005 If M represents the decrease in mass with the decrease in velocity, Mo is the value of the mass at rest, C is the velocity of light, v is the additional energy of motion  

                     v ^2 = MC ^2 / 0.5 Mo                     vN ^2 =M x C ^2 / o.5 x Mo

If M is equal to the mass loss in one nucleon = 0.0005, the mass weight of a nucleon at rest Mo = 1.0072761. The velocity of light C = 300000 Km per sec.

     vN = 2√10 ^-5 GeV x C / o.7 x 1 GeV = 2√10 ^-4 GeV x C /2.67

vN =-10 ^ -2 GeV x C / 1.42 = 0.01 / 2,67 x C  =0.01.42 x C = 0.14 x C

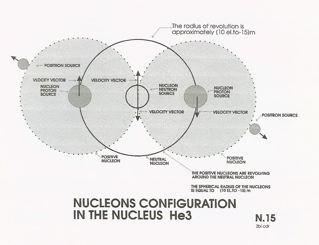
In the atom of the isotope H2 the velocity of revolution of two nucleons around each other must acquire a velocity of 0.031 x C shedding a mass equal to 0.0005 and maintain their nucleus requisites in mass. In following the same line of thought, we will now consider the isotope of Helium, He3, which has a nucleus with three nucleons that we assume to have a configuration as shown in sketch N.15. The nucleus of He3 is made by two protons and one neutron adding up to a mass weight of

1007825 + 1007825 + 1008650 = 3.0243

On the Aston mass spectrograph the mass weight of He3 is equal to 3.0160. The total mass shed into energy by the nucleus in the nuclear transformation is 0.0083. The mass lost by the neutron transforming into a nucleon is 0.001373. There must be (in order to complete the process of forming a nucleus) an additional mass weight loss by the nucleus equal to 0.0083 - 0.00137 = 0.007. The mass weight lost by each nucleon is then 0.007 / 3 = 0.002333. If we are assuming, as shown in our sketch N15, that the nucleons in He3 have a configuration consisting of one neutral nucleon sandwiched between two positive nucleons, the central neutral source is under the influence of the two positive sources acting on its velocity vector through their intensity impulses. Since the sources of the positive nucleons vectors are directed in opposite directions, their action must cancel, leaving the neutral nucleon free to proceed at its original transitional velocity.

In considering again the Lorentz formula

        M = 1/2 x Mo v2 / C2              vN = velocity of Nucleon N

        vN= 2 x MC2 / Mo = 2 x 10 ^-5 GeV C ^2 / C ^2  = 2 x 10 ^-5 C

If we make M equal to the mass lost by one nucleon = 0.002333.

Mo the value of the nucleon mass at rest = 1.0072761.

C the velocity of light = 300000 Km per sec equal to 1 in natural units.

v the increase in velocity 

        v2 = 2 x 0.002333 x 1.007276 x C2 / 1.0072761

          v2 = 2 x 0.002333 x C2 = 0.004666 x C2

            v =  √0.004666 x C2 = 0.068 C

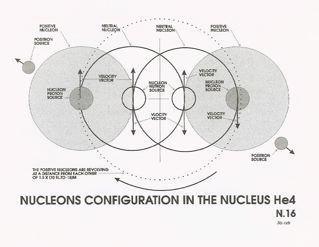
In the atom He3 the positive nucleons will revolve around the neutral nucleon at velocity equal to 0.068 C. Although the arrangement of the nucleons in the nucleus of an atom becomes more complicated with the increase in its atomic weight making our assumptions more tentative, we will try to describe the atom of Helium 4. (See sketch N18) We assume that the atom of He4 is composed (as indicated by its atomic number) by four nucleons, two of them being of a positive nature and two of neutral nature. The sum of two protons plus two neutrons adds up to a mass weight of 4.03295. On the Aston mass spectrograph the weight of He4 is shown to be 4.00260. The resulting mass weight loss by the nucleus is equal to 0.03035.

The mass of 2 neutrons is 2 x 1.008650 = 2.0173. The mass of 2 nucleons is 2 x 1.007276 = 2.0145. The total masses lost in the transformation of the two neutrons are 2.0173 - 2.0145 = 0.0028. The mass to be lost by 4 nucleons is 0.030 - 0.0028 = 0.027. The mass lost by each nucleon is 0.027 / 4 = 0.0068

       v2 = 2 x 0.0068 x 1.007276 x C2 / 1.007276 = 0.0136 x C2

                          v = 0.1l6 x C

The value of the additional velocity for He4 is equal to 0.116 x C. Assuming that the nucleus of Helium 4 is composed of 2 neutral nucleons sandwiched between 2 positive nucleons, these last must revolve around each other at a distance equal to 1.5 x 10-15 at a velocity equal to 0.116 x C over the original. The electrons and positrons in the atom are not affected by changes in the self-contained energy of the nucleons, but changes in their velocity are transmitted to the positron sources that are imprisoned in the nucleus by its implosion waves and are through them transferred to the electrons.

At its lower energy status the natural transitional velocity of a proton and of a single atom of hydrogen is 0.0044 x C.

The velocity of revolution in the nucleus of the isotope H2 is 0.031 x C.

The velocity of revolution in the nucleus of the isotope H3 is 0.068 x C.

The velocity of revolution in the nucleus of Helium H4 is 0.116 x C.